「無限に待てば価格はいずれ元に戻る」とすれば、「損切りせず、価格が上がったときにだけ利確」すれば負けないのでは？

この考えが正しければ、トレードは極めてシンプルになります。

つまり、損切りしなければ「負けなし」で期待値プラスになるはず！？

もしこの戦略が数学的に成立するならば、損切りは不要であり、トレードは耐え続けて利確するだけのゲームになります。

これは本当に可能なのか？今回は、この仮説を数式と確率を用いて検証します。

1. 損切りしなければ負けなし？

「損切りせず、利益確定だけをする」戦略を考えます。
この戦略は次のようなルールで成り立ちます。

価格がある一定値に達したら利確
価格が下がっても損切りせず、ひたすら待つ
無限に待てば価格は必ず元に戻るので、いずれ利益確定ができる

この戦略では、損切りしないため損失は発生せず、利益確定のチャンスだけを待つことができるはずです。

2. 期待リターン（期待値）の計算

この戦略で得られる利益の期待値 $E [R] を計算してみます。$
まず、利確と損切りの確率を考えます。
${利確確率：P}_{U} (x) = \frac{x - L}{U - L}$

${損切確率：P}_{L} (x) = \frac{U - x}{U - L}$

ここで、
xはエントリー時点の価格
U−xは利確ライン
x−Lは損切りライン
（しかし、損切りはしない）
損切りしないため、価格が $x- L に到達しても何もせず待ち続けます。$
つまり、損切り確率は 0 なので、期待値の損失の項目はなくなります。

すると期待値は、
$E [R] = (\frac{x - L}{U - L}) r$
ここで $r は、価格が$ $U に達したときの利益額です。$
この式を見るとすべて正の値で構成されているため、期待値は必ずプラスになります！

$x - L > 0$
（エントリー価格は損切りラインより大きい）
$U - L > 0$
$（利確ラインは損切りラインより上にある）$
$r > 0$
$（利確時には利益が確定する）$
したがって、この戦略は理論的には常にプラスの期待値を持つように見えます！

ということは、前回の話にあったラチェットのように、ランダムに見える相場で理論的には利益を出し続けることできるということでしょうか？

３. 本当に「無限に待てば勝てる」？

しかし、ここで重要な疑問が生じます。
「無限に待てば必ず戻る」という仮定は本当に正しいのでしょうか？
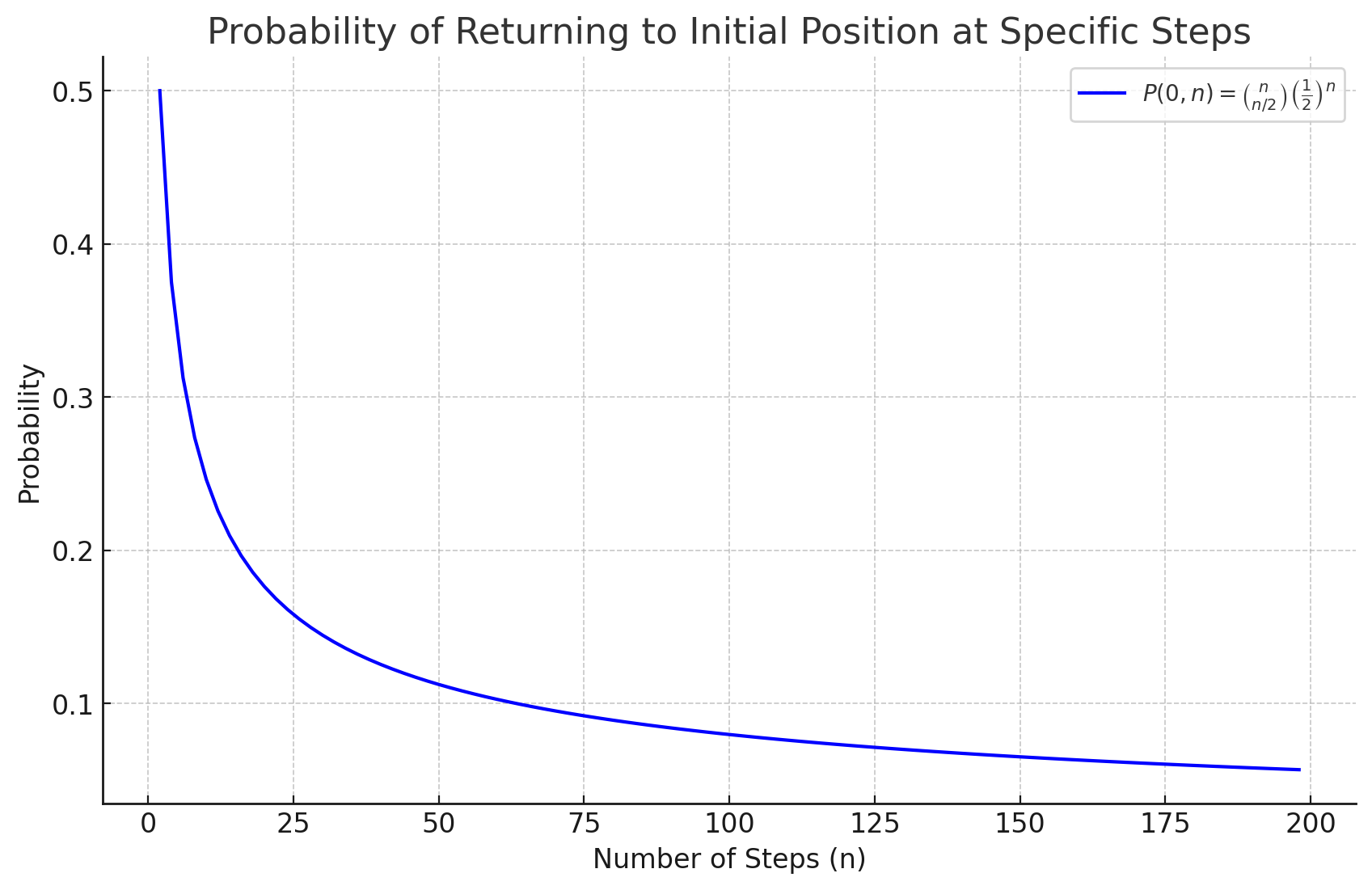
価格が「ちょうど元に戻る確率」は次の式で表されます。
$P (0, n) = (\binom{n}{n / 2}) {(\frac{1}{2})}^{n}$
これはnステップのうち、ちょうど半分が上昇・半分が下降する確率を示しています。
時間が経つほど、この確率はどんどん小さくなります。
この確率をグラフで確認しましょう。

４. グラフ：特定のステップで戻る確率

このグラフを見ると、ステップ数 $n$ が増えるにつれ、特定のステップで初期位置に戻る確率が急激に低下することがわかります。

短期間では、ある程度の確率で戻る可能性がある（例えば $n = 10$ では戻る確率が比較的高い）。
長期になると、1回の特定のステップでちょうど元に戻る確率はほぼゼロに近づく。

つまり、時間が経つほど「ある特定のタイミングで戻ることを期待するのは極めて難しい」ということになります。

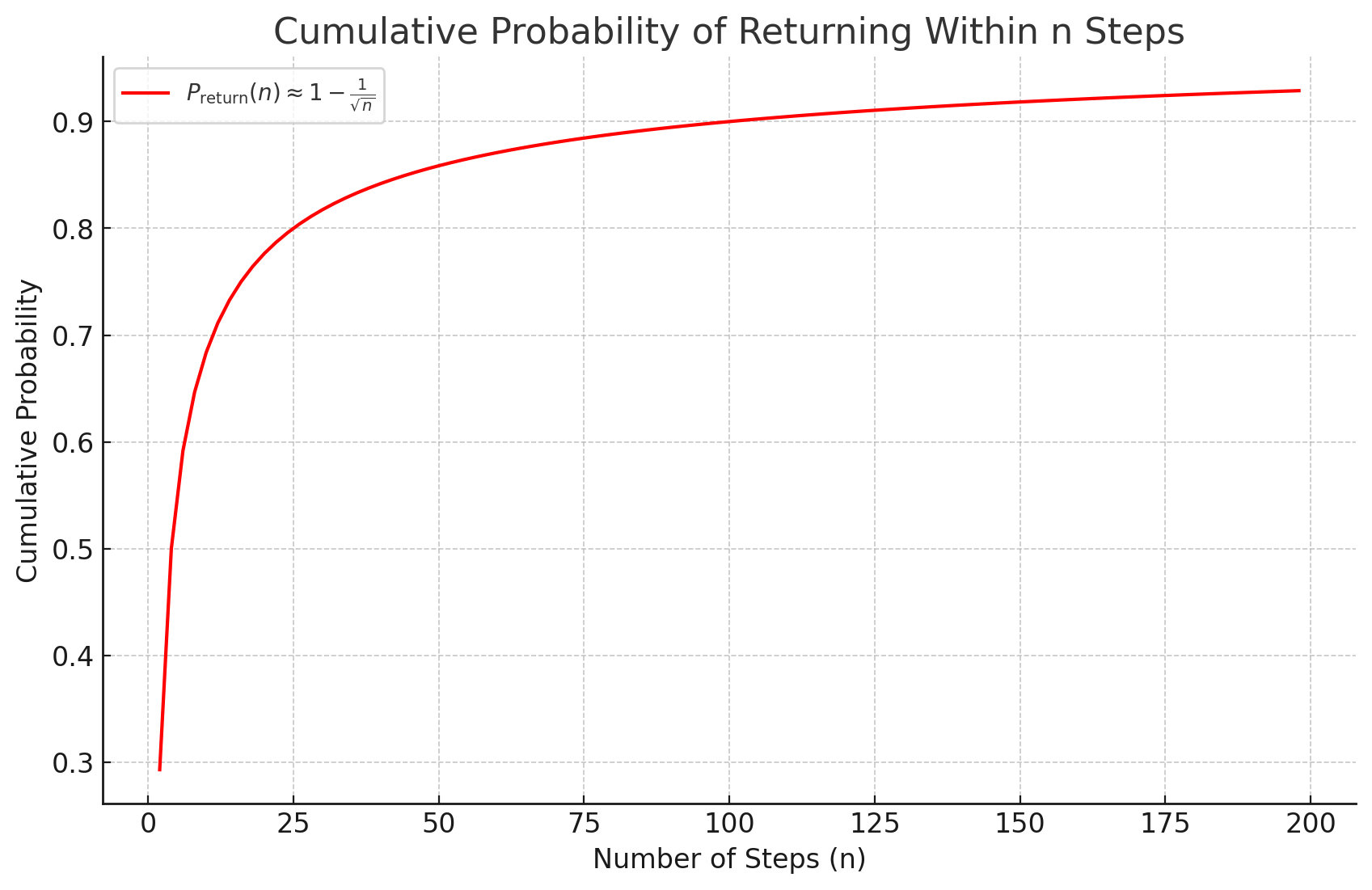
５. 累積的な戻る確率を考える

しかし、トレーダーとしては 「ある特定の瞬間に戻るか」ではなく、「いつかは戻るのか」 が重要です。
そこで、「ある時間以内に1回でも元に戻る確率」 を考えます。

この確率は次の式で近似されます。

$P_{\text{return}}(n) \approx 1 - \frac{1}{\sqrt{n}}$

6．累積的な戻る確率

このグラフは、「ある時間以内に1回でも初期位置に戻る確率」を示しています。

時間が長くなるにつれて、確率は 1 に近づく。
つまり、「無限に待てば戻る確率は 1」であることがわかります。

しかし、ここで問題となるのは次の点です。

短期間では戻らない確率も高い。
例えば、 $n = 10$ では戻る確率はまだ 0.7 程度であり、完全には保証されない

7.ポリヤの再帰定理（Polya's Recurrence Theorem）

ここまでのグラフと計算を見て、以下の事実が直感的に理解できるはずです。

累積的な確率を見ると、時間が無限にあれば「いつかは戻る」確率が 1 に近づく。

これを数学的に厳密に証明したのが、ポリヤの再帰定理（Polya's Recurrence Theorem）です。

ポリヤの再帰定理（G. Polya, 1921）
1次元のランダムウォークでは、無限の時間があれば初期位置に戻る確率は 1 である。
$\lim_{n \to \infty} P_{return} (n) = 1$

これは、「無限に待てば必ず戻る」ことを数学的に保証しています。

8. しかし、現実ではこの戦略は成り立たない

「無限に待てば戻る」という事実が分かりましたが、これがトレード戦略として有効かどうかは別の問題です。

決定的な問題は、「戻るまでにかかる時間の期待値が無限大になる」ことです。

価格が元の位置に戻るまでの期待時間は、次のように近似されます。

$E [T] \approx n^{2}$

例えば、

$n = 10$ の場合、戻るまでの平均時間は $10^{2} = 100$ ステップ。
$n = 100$ の場合、戻るまでの平均時間は $100^{2} = 10, 000$ ステップ。

つまり、価格が元に戻るまでの時間は指数的に増加するため、「無限に待つ」間に資金、または寿命が尽きるリスクが高いのです。投資ファンドはこの問題を、膨大な資金、寿命のない法人で解決しているのですね。

8. 結論

理論的には、無限に待てば価格は必ず元に戻る。
しかし、特定のステップで元の位置に戻る確率は、時間が経つにつれて急激に低下する。
価格が戻るまでの期待時間は $n^{2}$ に比例して増加するため、資金、時間が尽きる可能性が高い。

したがって、「無限に待てば戻る」戦略は数学的には正しいが、現実のトレードには適用しづらいという結論になります。

次回は、「有限時間内で期待値を向上させるには？」について考察していきます。

第3回：塩漬けは正義か！？待っていれば価格は戻るのか？